Проблема

В прошлой статье мы построили бинарное дерево поиска и реализовали основные операции (вставка, удаление, поиск). Выгода использования такого дерева - сокращение итераций для поиска. При нахождении ключа в связанном списке, сложность в худшем случае будет составять O(n), в то время как при нахождении ключа в бинарном дерево сложность будет O(logn). Однако, существует вероятность когда наше дерево будет иметь такую же сложность обхода как и связанный список.

Как видно из примера, дерево плавно превратилось в список, т.к. при добавлении новых узлов все они меньше предыдущих, следовательно мы вынуждены добавлять их к левым потомкам. Для решения данной проблемы придумали сбалансированные деревья.

Решение

Сбалансированное дерево - бинарное дерево поиска, в котором для каждой из вершин высота поддеревье отличается не более чем на 1.

Если ключи известны заранее то построить сбалансированное дерево можно достаточно просто. Отсортируем список ключей, возьмем значение по медиане в качестве корня деревоа, далее итерируемся по левой и правой части и вставляем узлы.

В данной статье будут рассмотрены АВЛ деревья. Такие деревья перестраиваются путем левого и правого поворота относительно узла при операциях вставки и удаления.

Перед началом балансировки необходимо расширить структуру Node. Добавим фактор бааланса.

type Node struct {
    key int
    left *Node
    right *Node
    parent *Node
    balance int
}

В данном случае, баланс - это разница между количество левых и правх поддеревьев. Высчитывать баланс можно при вставке/удалении узла, а также асинхронно, проходясь по всем узлам. Я буду делать перерасчет баланса при вставке/удалении.

Введение данного фактора позволит узнать, какие узлы будут повернуты и куда. Поворот будет осуществляться если модуль от баланса больше 1.

Как реализовать проверку баланса? Я не нашел описание этого алгоритма в сети, но немного порисовав кружечки, пришел к такому решению:

1. Вставка - вставляем элемент (точно также как в предыдущей статье), затем поднимается вверх и инкрементируем баланс если текущий ключ больше родительского, либо декрементируем если меньше. Останавливаем операцию если отсутствует родительский узел, либо у соседнего поддерева большее количество элементов (проверяем баланс родителя, если отрицательный то слева больше потомков, если положительный - то справа)

   TODO: проверить алгоритм удаления

2. Удаление - в случае если у удаляемого узла 1 потомок или их нет, начинаем перерасчет баланса от родителя и выше. Если потомка 2 то начинаем перерасчет баланса еще и для самого маленького узла в родительском дереве.

Реализуем функцию ребалансировки

// Функция ребалансировки относительно текущего узла, принимает 1 на добавление узла -1 на удаление
func (n *Node) recalculateBalance(direction int) {
    currentNode := n

    for currentNode.parent != nil {
        balance := 1 * direction
        if currentNode.key < currentNode.parent.key {
            balance = -1 * direction
        }
        currentNode.parent.balance += balance
        if direction == 1 && currentNode.parent.balance == 0 ||
            direction == -1 &&
            currentNode.parent.left != nil &&
            currentNode.parent.right != nil &&
            (currentNode.parent.balance - balance >= 0 && currentNode.parent.balance > 0 || currentNode.parent.balance - balance < 0 && currentNode.parent.balance < 0) {
            break
        }

        currentNode = currentNode.parent
    }
}

Данная функция ведет перерасчет от текущего узла вверх. Теперь давайте расширим функцию добавления, реализованную в предыдущей статье, метод findParentNode там же.

func (n *Node) Insert(key int) *Node {
    newNode := &Node{
        key: key,
    }
    lastNode := n.findParentNode(key)
    if lastNode.key == key {
        return lastNode
    }
    newNode.parent = lastNode

    nextNode := lastNode.selectNextNode(key)
    *nextNode = newNode
    newNode.recalculateBalance(1)
    return newNode.balanceTree()
}

Функцияюбалансировки реализуем немного позже. Давайте рассмотрим как расставляется баланс для деревьев при добавлении новых узлов. (баланс в скобочках)

Следующим шагом реализуем ребалансировку для метода удаления. Как мы уже выяснили, для удаления существует 3 различных сценария:

1. У узла отсутствуют потомки
2. У узла 1 потомок
3. У узла 2 потомка

Делать ребалансировку будем исходя из этого. Для первого случая необходимо лишь изменить баланс у родителя, т.к. потомки отсутствуют то фактор баланса будет равен 0.

Во втором случае необходимо запустить функцию пересчета баланса для с флагом -1 (т.к. прозоишло удаление) для родительского узла.

В 3 случае мы присваиваем правому поддереву баланс текущего - 1, функцию ребалансировки запускаем в случае если правое поддерево было максимальным по длине (баланс > 1).

Рассмотрим полученный код

func (n *Node) Remove(key int) *Node {
    if key < n.key {
        return n.left.Remove(key)
    }
    if key > n.key {
        return n.right.Remove(key)
    }

    nextNode := n.parent.selectNextNode(key)
    // Первый случай, у узла нет потомков
    if n.left == nil && n.right == nil {
        *nextNode = nil
        n.parent.balance = 0
        n.parent.recalculateBalance(-1)
        return n.parent.balanceTree()
    }

    // Второй случай, у зла 1 потомок
    if n.left == nil {
        *nextNode = n.right
        n.right.parent = n.parent
        n.right.recalculateBalance(-1)
        return n.right.balanceTree()
    }

    if n.right == nil {
        *nextNode = n.left
        n.left.parent = n.parent
        n.left.recalculateBalance(-1)
        return n.left.balanceTree()
    }

    // 3 случай, у удаляемого узла 2 потомка
    maxLeftNode := n.right
    for {
        if maxLeftNode.left == nil {
            break
        }
        maxLeftNode = n.right.left
    }

    maxLeftNode.left = n.left
    n.left.parent = maxLeftNode

    n.right.parent = n.parent
    n.right.balance = n.balance - 1
    // Перерасчитываем баланс для родителя, если правое поддерево было максимальным по длине
    if n.balance > 0 && n.right.balance <= 0 {
        n.right.recalculateBalance(-1)
    }
    *nextNode = n.right
    return n.right.balanceTree()
}

Теперь можем реализовать метод balanceTree, перед этим рекомендую немного порисовать граф и то как можно его балансировать.

Для баланса дерева используются левое и правое вращение (а также их комбинация).

Малое левое вращенние. Применяется когда баланс равен 2

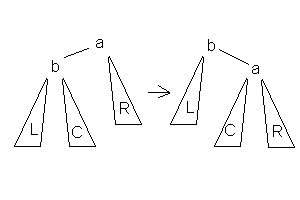
Малое правое вращение. Применяется когда фактор баланса равен -2

Большое левое вращение. Применяется когда фактор баланса равен 2 и фактор баланса правого поддерева меньше 0

Большое правое вращение. Применяется когда фактор баланса равен 2 и фактор баланса левого поддерева меньше 0.

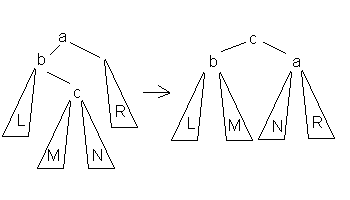
Рассмотрим на конкретном примере

Реализуем малый левый и правый повороты:

func (n *Node) rotateLeft() *Node {
    p := n.right
    p.parent = n.parent
    if n.parent != nil {
        parent := n.parent.selectNextNode(n.key)
        *parent = p
    }
    n.right = p.left
    if p.left != nil {
        p.left.parent = n
    }

    p.left = n
    n.parent = p


    n.balance = 0
    p.balance -= 1
    p.recalculateBalance(-1)
    return p
}


func (n *Node) rotateRight() *Node {
    q := n.left
    q.parent = n.parent
    parent := n.parent.selectNextNode(n.key)
    *parent = q
    n.left = q.right
    if q.right != nil {
        q.right.parent = n
    }

    q.right = n
    n.parent = q


    n.balance = 0
    q.balance += 1
    q.recalculateBalance(+1)
    return q
}

Реализуем поворот в зависимости от фактора баланса:

func (n *Node) balanceTree() *Node {
    currentNode := n
    for {
        if currentNode.balance == 2 {
            if currentNode.right.balance < 0 {
                currentNode.right = currentNode.right.rotateRight()
            }
            currentNode = currentNode.rotateLeft()
            break
        }
        if currentNode.balance == -2 {
            if currentNode.left.balance > 0 {
                currentNode.left = currentNode.left.rotateLeft()
            }
            currentNode = currentNode.rotateRight()
            break
        }


        if currentNode.parent == nil {
            break
        }

        currentNode = currentNode.parent
    }

    return currentNode.findRootNod()
}

Также стоит отметить, что при вращении корневой элемент может быть изменен, поэтому после каждой операции возвращаем корневой элемент (тот у которого нет родительского узла).

Потыкать реализацию можно тут, скачать исходники сдесь